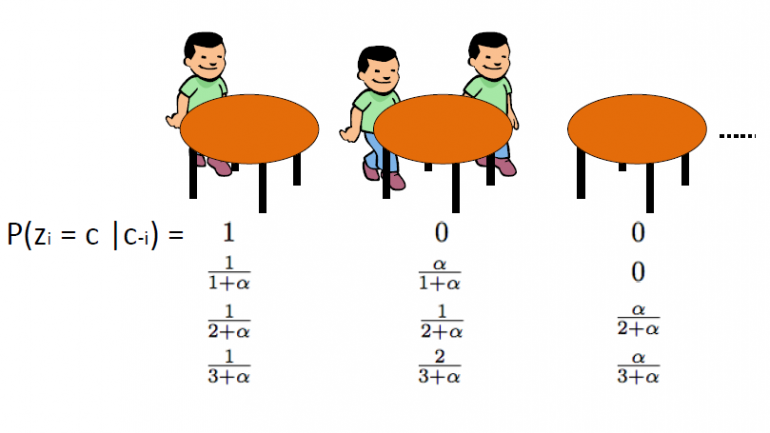The Dirichlet Course of the Chinese language Restaurant Course of and different representations

This text is the third a part of the collection on Clustering with Dirichlet Course of Combination Fashions. The earlier time we outlined the Finite Combination Mannequin primarily based on Dirichlet Distribution and we posed questions on how we are able to make this explicit mannequin infinite. We briefly mentioned the concept of taking the restrict of the mannequin when the ok variety of clusters tends to infinity however as we harassed the existence of such an object shouldn’t be trivial (in different phrases, how can we truly “take the restrict of a mannequin”?). As a reminder, the explanation why we wish to take make ok infinite is as a result of on this approach we may have a non-parametric mannequin which doesn’t require us to predefine the full variety of clusters inside the information.

Replace: The Datumbox Machine Studying Framework is now open-source and free to obtain. Take a look at the bundle com.datumbox.framework.machinelearning.clustering to see the implementation of Dirichlet Course of Combination Fashions in Java.

Despite the fact that our goal is to construct a mannequin which is able to performing clustering on datasets, earlier than that we should talk about about Dirichlet Processes. We are going to present each the strict mathematical definitions and the extra intuitive explanations of DP and we’ll talk about methods to assemble the method. These constructions/representations will be seen as a method to discover occurrences of Dirichlet Course of in “actual life”.

Even if I attempted to adapt my analysis report in such a approach in order that these weblog posts are simpler to observe, it’s nonetheless essential to outline the required mathematical instruments and distributions earlier than we soar into utilizing the fashions. Dirichlet Course of fashions are a subject of energetic analysis, however they do require having an excellent understanding of Statistics and Stochastic Processes earlier than utilizing them. One other drawback is that as we’ll see on this article, Dirichlet Processes will be represented/constructed with quite a few methods. Consequently a number of educational papers use utterly completely different notation/conventions and study the issue from completely different factors of view. On this publish I attempt to clarify them so simple as potential and use the identical notation. Hopefully issues will change into clearer with the 2 upcoming articles which concentrate on the definition of Dirichlet Course of Combination Fashions and on learn how to truly use them to carry out cluster evaluation.

1. Definition of Dirichlet Course of

A Dirichlet course of over a Θ area is a stochastic course of. It’s a likelihood distribution over “likelihood distributions over Θ area” and a draw from it’s a discrete distribution. Extra formally a Dirichlet Distribution is a distribution over likelihood measures. A likelihood measure is a perform of subsets of area Θ to [0,1]. G is a DP distributed random likelihood measure, denoted as , if for any partition (A₁,…A_n) of area Θ now we have that .

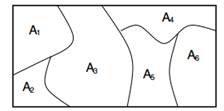
Determine 1: Marginals on finite partitions are Dirichlet distributed.

The DP has two parameters: The primary one is the bottom distribution G₀ which serves like a imply . The second is the power parameter α which is strictly optimistic and serves like inverse-variance . It determines the extent of the repetition of the values of the output distribution. The upper the worth of a, the smaller the repetition; the smaller the worth, the upper the repetition of the values of output distribution. Lastly the Θ area is the parameter area on which we outline the DP. Furthermore the area Θ can be the definition area of G₀ which is identical because the one in every of G.

An easier and extra intuitive approach to elucidate a Dirichlet Course of is the next. Suppose that now we have an area Θ that may be partitioned in any finite approach (A₁,…,A_n) and a likelihood distribution G which assigns possibilities to them. The G is a particular likelihood distribution over Θ however there are a lot of others. The Dirichlet Course of on Θ fashions precisely this; it’s a distribution over all potential likelihood distributions on area Θ. The Dirichlet course of is parameterized with the G₀ base perform and the α focus parameter. We will say that G is distributed in keeping with DP with parameters α and G₀ if the joint distribution of the possibilities that G assigns to the partitions of Θ follows the Dirichlet Distribution. Alternatively we are able to say that the possibilities that G assigns to any finite partition of Θ follows Dirichlet Distribution.

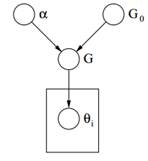
Determine 2: Graphical Mannequin of Dirichlet Course of

Lastly above we are able to see the graphical mannequin of a DP. We must always observe that α is a scalar hyperparameter, G₀ is the bottom distribution of DP, G a random distribution over Θ parameter area sampled from the DP which assigns possibilities to the parameters and θ_i is a parameter vector which is drawn from the G distribution and it is a component of Θ area.

2. Posterior Dirichlet Processes

The Posterior Dirichlet Processes had been mentioned by Ferguson. We begin by drawing a random likelihood measure G from a Dirichlet Course of, . Since G is a likelihood distribution over Θ we are able to additionally pattern from this distribution and draw impartial identically distributed samples θ₁,…, θ_n ~ G. Since attracts from a Dirichlet Course of are discrete distributions, we are able to signify the place is a brief notation for which is a delta perform that takes 1 if and 0 elsewhere. An fascinating impact of that is that since G is outlined this manner, there’s a optimistic likelihood of various samples having the identical worth . As we’ll see afterward, this creates a clustering impact that can be utilized to carry out Cluster Evaluation on datasets.

By utilizing the above definitions and observations we wish to estimate the posterior of the Dirichlet Course of given the samples θ. Nonetheless since we all know that and by utilizing the Bayes Guidelines and the Conjugacy between Dirichlet and Multinomial now we have that and .

Equation 1: Posterior Dirichlet Course of

This property is essential and it’s utilized by the varied DP representations.

3. Dirichlet Course of representations

Within the earlier segments we outlined the Dirichlet Course of and introduced its theoretical mannequin. One essential query that we should reply is how do we all know that such an object exists and the way we are able to assemble and signify a Dirichlet Course of.

The primary indications of existence was offered by Ferguson who used the Kolmogorov Consistency Theorem, gave the definition of a Dirichlet Course of and described the Posterior Dirichlet Course of. Persevering with his analysis, Blackwell and MacQueen used the de Finetti’s Theorem to show the existence of such a random likelihood measure and launched the Blackwell-MacQueen urn scheme which satisfies the properties of Dirichlet Course of. In 1994 Sethuraman offered an extra easy and direct approach of establishing a DP by introducing the Stick-breaking building. Lastly one other illustration was offered by Aldous who launched the Chinese language Restaurant Course of as an efficient method to assemble a Dirichlet Course of.

The varied Representations of the Dirichlet Course of are mathematically equal however their formulation differs as a result of they study the issue from completely different factors of view. Beneath we current the most typical representations discovered within the literature and we concentrate on the Chinese language Restaurant Course of which offers a easy and computationally environment friendly method to assemble inference algorithms for Dirichlet Course of.

3.1 The Blackwell-MacQueen urn scheme

The Blackwell-MacQueen urn scheme can be utilized to signify a Dirichlet Course of and it was launched by Blackwell and MacQueen. It’s primarily based on the Pólya urn scheme which will be seen as the other mannequin of sampling with out alternative. Within the Pólya urn scheme we assume that now we have a non-transparent urn that accommodates coloured balls and we draw balls randomly. After we draw a ball, we observe its coloration, we put it again within the urn and we add an extra ball of the identical coloration. An analogous scheme is utilized by Blackwell and MacQueen to assemble a Dirichlet Course of.

This scheme produces a sequence of θ₁,θ₂,… with conditional possibilities . On this scheme we assume that G₀ is a distribution over colours and every θ_n represents the colour of the ball that’s positioned within the urn. The algorithm is as follows:

· We begin with an empty urn.

· With likelihood proportional to α we draw and we add a ball of this coloration within the urn.

· With likelihood proportional to n-1 we draw a random ball from the urn, we observe its coloration, we place it again to the urn and we add an extra ball of the identical coloration within the urn.

Beforehand we began with a Dirichlet Course of and derived the Blackwell-MacQueen scheme. Now let’s begin reversely from the Blackwell-MacQueen scheme and derive the DP. Since θ_i had been drawn in an iid method from G, their joint distribution shall be invariant to any finite permutations and thus they’re exchangeable. Consequently by utilizing the de Finetti’s theorem, now we have that there should exist a distribution over measures to make them iid and this distribution is the Dirichlet Course of. Consequently we show that the Blackwell-MacQueen urn scheme is a illustration of DP and it provides us a concrete method to assemble it. As we’ll see later, this scheme is mathematically equal to the Chinese language Restaurant Course of.

3.2 The Stick-breaking building

The Stick-breaking building is an alternate method to signify a Dirichlet Course of which was launched by Sethuraman. It’s a constructive approach of forming the distribution and makes use of the following analogy: We assume that now we have a stick of size 1, we break it at place β₁ and we assign π₁ equal to the size of the a part of the stick that we broke. We repeat the identical course of to acquire π₂, π₃,… and so on; because of the approach that this scheme is outlined we are able to proceed doing it infinite occasions.

Based mostly on the above the π_ok will be modeled as , the place the whereas as within the earlier schemes the θ are sampled immediately by the Base distribution . Consequently the G distribution will be written as a sum of delta capabilities weighted with π_ok possibilities which is the same as . Thus the Stick-breaking building provides us a easy and intuitively method to assemble a Dirichlet Course of.

3.3 The Chinese language Restaurant Course of

The Chinese language Restaurant Course of, which was launched by Aldous, is one other efficient method to signify a Dirichlet Course of and it may be immediately linked to Blackwell-MacQueen urn scheme. This scheme makes use of the following analogy: We assume that there’s a Chinese language restaurant with infinite many tables. As the shoppers enter the restaurant they sit randomly to any of the occupied tables or they select to sit down to the primary obtainable empty desk.

The CRP defines a distribution on the area of partitions of the optimistic integers. We begin by drawing θ₁,…θ_n from Blackwell-MacQueen urn scheme. As we mentioned within the earlier segments, we count on to see a clustering impact and thus the full variety of distinctive θ values ok shall be considerably lower than n. Thus this defines a partition of the set {1,2,…,n} in ok clusters. Consequently drawing from the Blackwell-MacQueen urn scheme induces a random partition of the {1,2,…,n} set. The Chinese language Restaurant Course of is that this induced distribution over partitions. The algorithm is as follows:

· We begin with an empty restaurant.

· The 1^st buyer sits at all times on 1^st desk

· The n+1^th buyer has 2 choices:

o Sit on the first unoccupied desk with likelihood

o Sit on any of the kth occupied tables with likelihood
the place is the variety of folks sitting on that desk

The place α is the dispersion worth of DP and n is the full variety of clients within the restaurant at a given time. The latent variable z_i shops the desk variety of the i^th buyer and takes values from 1 to ok_n the place ok_n is the full variety of occupied tables when n clients are within the restaurant. We must always observe that the ok_n will at all times be much less or equal to n and on common it’s about . Lastly we should always observe that the likelihood of desk association is invariant to permutations. Thus the z_i is exchangeable which suggests that tables with identical measurement of shoppers have the identical likelihood.

The Chinese language Restaurant Course of is strongly linked to Pólya urn scheme and Dirichlet Course of. The CRP is a method to specify a distribution over partitions (desk assignments) of n factors and can be utilized as a previous on the area of latent variable z_i which determines the cluster assignments. The CRP is equal to Pólya’s urn scheme with solely distinction that it doesn’t assign parameters to every desk/cluster. To go from CRP to Pólya’s urn scheme we draw for all tables ok=1,2… after which for each x_i which is grouped to desk z_i assign a . In different phrases assign to the brand new x_i the parameter θ of the desk. Lastly since we are able to’t assign the θ to infinite tables from the start, we are able to simply assign a brand new θ each time somebody sits on a brand new desk. Resulting from all of the above, the CRP can assist us construct computationally environment friendly algorithms to carry out Cluster Evaluation on datasets.

On this publish, we mentioned the Dirichlet Course of and a number of other methods to assemble it. We are going to use the above concepts within the subsequent article. We are going to introduce the Dirichlet Course of Combination Mannequin and we’ll use the Chinese language Restaurant Illustration to be able to assemble the Dirichlet Course of and preform Cluster Evaluation. For those who missed few factors don’t fear as issues will begin changing into clearer with the subsequent two articles.

I hope you discovered this publish fascinating. For those who did, take a second to share it on Fb and Twitter. 🙂