The Dirichlet Course of Combination Mannequin

This weblog put up is the fourth a part of the collection on Clustering with Dirichlet Course of Combination Fashions. In earlier articles we mentioned the Finite Dirichlet Combination Fashions and we took the restrict of their mannequin for infinite okay clusters which led us to the introduction of Dirichlet Processes. As we noticed, our goal is to construct a combination mannequin which doesn’t require us to specify the variety of okay clusters/parts from the start. After presenting completely different representations of Dirichlet Processes, it’s now time to truly use DPs to assemble an infinite Combination Mannequin that allow us to carry out clustering. The goal of this text is to outline the Dirichlet Course of Combination Fashions and focus on using Chinese language Restaurant Course of and Gibbs Sampling. In case you have not learn the earlier posts, it’s extremely really useful to take action as the subject is a bit theoretical and requires good understanding on the development of the mannequin.

Replace: The Datumbox Machine Studying Framework is now open-source and free to obtain. Take a look at the package deal com.datumbox.framework.machinelearning.clustering to see the implementation of Dirichlet Course of Combination Fashions in Java.

1. Definition of Dirichlet Course of Combination Mannequin

Utilizing Dirichlet Processes permits us to have a combination mannequin with infinite parts which will be thought as taking the restrict of the finite mannequin for okay to infinity. Let’s assume that we’ve the next mannequin:

Equation 1: Dirichlet Course of Combination Mannequin

The place G is outlined as and used as a brief notation for which is a delta operate that takes 1 if and 0 elsewhere. The θ_i are the cluster parameters that are sampled from G. The generative distribution F is configured by cluster parameters θ_i and is used to generate x_i observations. Lastly we are able to outline a Density distribution which is our combination distribution (countable infinite combination) with mixing proportions and mixing parts .

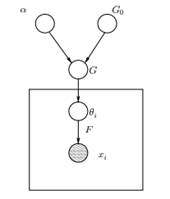
Determine 1: Graphical Mannequin of Dirichlet Course of Combination Mannequin

Above we are able to see the equal Graphical Mannequin of the DPMM. The G₀ is the bottom distribution of DP and it’s often chosen to be conjugate previous to our generative distribution F so as to make the computations simpler and make use of the interesting mathematical properties. The α is the scalar hyperparameter of Dirichlet Course of and impacts the variety of clusters that we’ll get. The bigger the worth of α, the extra the clusters; the smaller the α the less clusters. We should always observe that the worth of α expresses the energy of imagine in G₀. A big worth signifies that many of the samples shall be distinct and have values focused on G₀. The G is a random distribution over Θ parameter area sampled from the DP which assigns possibilities to the parameters. The θ_i is a parameter vector which is drawn from the G distribution and comprises the parameters of the cluster, F distribution is parameterized by θ_i and x_i is the information level generated by the Generative Distribution F.

It is very important observe that the θ_i are components of the Θ parameter area they usually “configure” our clusters. They can be seen as latent variables on x_i which inform us from which element/cluster the x_i comes from and what are the parameters of this element. Thus for each x_i that we observe, we draw a θ_i from the G distribution. With each draw the distribution modifications relying on the earlier picks. As we noticed within the Blackwell-MacQueen urn scheme the G distribution will be built-in out and our future picks of θ_i rely solely on G₀: . Estimating the parameters θi from the earlier system is just not all the time possible as a result of many implementations (reminiscent of Chinese language Restaurant Course of) contain the enumerating via the exponentially rising okay parts. Thus approximate computational strategies are used reminiscent of Gibbs Sampling. Lastly we should always observe that despite the fact that the okay clusters are infinite, the variety of lively clusters is . Thus the θ_i will repeat and exhibit a clustering impact.

2. Utilizing the Chinese language Restaurant Course of to outline an Infinite Combination Mannequin

The mannequin outlined within the earlier section is mathematically stable, nonetheless it has a serious downside: for each new x_i that we observe, we should pattern a brand new θ_i bearing in mind the earlier values of θ. The issue is that in lots of circumstances, sampling these parameters is usually a troublesome and computationally costly activity.

An alternate strategy is to make use of the Chinese language Restaurant Course of to mannequin the latent variables z_i of cluster assignments. This manner as a substitute of utilizing θ_i to indicate each the cluster parameters and the cluster assignments, we use the latent variable z_i to point the cluster id after which use this worth to assign the cluster parameters. Because of this, we not have to pattern a θ each time we get a brand new commentary, however as a substitute we get the cluster project by sampling z_i from CRP. With this scheme a brand new θ is sampled solely when we have to create a brand new cluster. Beneath we current the mannequin of this strategy:

Equation 2: Combination Mannequin with CRP

The above is a generative mannequin that describes how the information x_i and the clusters are generated. To carry out the cluster evaluation we should use the observations x_i and estimate the cluster assignments z_i.

3. Combination Mannequin Inference and Gibbs Sampling

Sadly since Dirichlet Processes are non-parametric, we can’t use EM algorithm to estimate the latent variables which retailer the cluster assignments. As a way to estimate the assignments we’ll use the Collapsed Gibbs Sampling.

The Collapsed Gibbs Sampling is an easy Markov Chain Monte Carlo (MCMC) algorithm. It’s quick and permits us to combine out some variables whereas sampling one other variable. However this algorithms requires us to pick a G₀ which is a conjugate prior of F generative distribution so as to have the ability to remedy analytically the equations and have the ability to pattern straight from .

The steps of the Collapsed Gibbs Sampling that we’ll use to estimate the cluster assignments are the next:

• Initialize the z_i cluster assignments randomly
• Repeat till convergence
• Choose randomly a x_i
  
• Maintain the opposite z_j mounted for each j≠i:
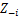
• Assign a brand new worth on z_i by calculating the “CRP chance” that is dependent upon z_j and x_j of all j≠i:

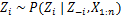
Within the subsequent article we’ll concentrate on carry out cluster evaluation through the use of Dirichlet Course of Combination fashions. We are going to outline two completely different Dirichlet Course of Combination Fashions which use the Chinese language Restaurant Course of and the Collapsed Gibbs Sampling so as to carry out clustering on steady datasets and paperwork.