November 14, 2019
Final night time on the practice I learn this good paper by David Duvenaud and colleagues. Round midnight I acquired a calendar notification “it is David Duvenaud’s birthday”. So I assumed it is time for a David Duvenaud birthday particular (do not get too excited David, I will not make it an annual custom…)
Background
I lately coated iMAML: the meta-learning algorithm that makes use of implicit gradients to sidestep backpropagating by the internal loop optimization in meta-learning/hyperparameter tuning. The tactic introduced in (Lorraine et al, 2019) makes use of the identical high-level concept, however introduces a special – on the floor much less fiddly – approximation to the essential inverse Hessian. I will not spend quite a lot of time introducing the entire meta-learning setup from scratch, you need to use the earlier put up as a place to begin.
Implicit Operate Theorem
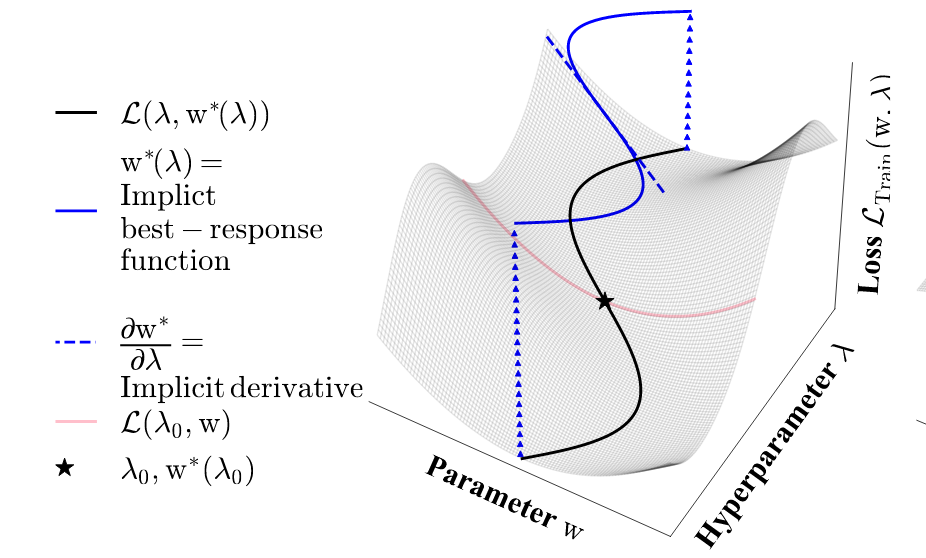
Many – although not all – meta-learning or hyperparameter optimization issues will be said as nested optimization issues. If we’ve some hyperparameters $lambda$ and a few parameters $theta$ we’re considering
$$
operatorname{argmin}_lambda mathcal{L}_V (operatorname{argmin}_theta mathcal{L}_T(theta, lambda)),
$$
The place $mathcal{L}_T$ is a few coaching loss and $mathcal{L}_V$ a validation loss. The optimum parameter to the coaching downside, $theta^ast$ implicitly depends upon the hyperparameters $lambda$:
$$
theta^ast(lambda) = operatorname{argmin} f(theta, lambda)
$$
If this implicit operate mapping $lambda$ to $theta^ast$ is differentiable, and topic to another situations, the implicit operate theorem states that its spinoff is
$$
left.frac{partialtheta^{ast}}{partiallambda}rightvert_{lambda_0} = left.-left[frac{partial^2 mathcal{L}_T}{partial theta partial theta}right]^{-1}frac{partial^2mathcal{L}_T}{partial theta partial lambda}rightvert_{lambda_0, theta^ast(lambda_0)}
$$
The system we obtained for iMAML is a particular case of this the place the $frac{partial^2mathcal{L}_T}{partial theta partial lambda}$ is the id It is because there, the hyperparameter controls a quadratic regularizer $frac{1}{2}|theta – lambda|^2$, and certainly in case you differentiate this with respect to each $lambda$ and $theta$ you’re left with a relentless instances id.
The first problem after all is approximating the inverse Hessian, or certainly matrix-vector merchandise involving this inverse Hessian. That is the place iMAML and the strategy proposed by Lorraine et al, (2019) differ. iMAML makes use of a conjugate gradient technique to iteratively approximate the gradient. On this work, they use a Neumann sequence approximation, which, for a matrix $U$ appears as follows:
$$
U^{-1} = sum_{i=0}^{infty}(I – U)^i
$$
That is mainly a generalization of the higher identified sum of a geometrical sequence: if in case you have a scalar $vert u vert<1$ then
$$
sum_{i=0}^infty q^i = frac{1}{1-q}.
$$
Utilizing a finite truncation of the Neumann sequence one can approximate the inverse Hessian within the following method:
$$
left[frac{partial^2 mathcal{L}_T}{partial theta partial theta}right]^{-1} approx sum_{i=1}^j left(I – frac{partial^2 mathcal{L}_T}{partial theta partial theta}proper)^i.
$$
This Neumann sequence approximation, a minimum of on the floor, appears considerably much less trouble to implement than working a conjugate gradient optimization step.
Experiments
One of many enjoyable bits of this paper is the attention-grabbing set of experiments the authors used to show the flexibility of this method. For instance, on this framework, one can deal with the coaching dataset as a hyperparameter. Optimizing pixel values in a small coaching dataset, one picture per class, allowed the authors to “distill” a dataset right into a set of prototypical examples. When you practice your neural internet on this distilled dataset, you get comparatively good validation efficiency. The outcomes aren’t fairly as image-like as one would think about, however for some lessons, like bikes, you even get recognisable shapes:
In one other experiment the authors skilled a community to carry out information augmentation, treating parameters of this community as a hyperparameter of a studying activity. In each of those circumstances, the variety of hyperparameters optimized have been within the a whole lot of 1000’s, method past the quantity we often contemplate as hyperparameters.
Limitations
This technique inherits a few of the limitations I already mentioned with iMAML. Please additionally see the feedback the place varied folks gave tips to work that overcomes a few of these limitations.
Most crucially, strategies primarily based on implicit gradients assume that your studying algorithm (internal loop) finds a novel, optimum parameter that minimises some loss operate. That is merely not a legitimate assumption for SGD the place totally different random seeds would possibly produce very totally different and in another way behaving optima.
Secondly, this assumption solely permits for hyperparameters that management the loss operate, however not for ones that management different points of the optimization algorithm, resembling studying charges, batch sizes or initialization. For these form of conditions, express differentiation should still be probably the most aggressive resolution. On that be aware, I additionally suggest studying this latest paper on generalized inner-loop meta-learning and the related pytorch bundle greater.
Conclusion
Pleased birthday David. Good work!