- April 7, 2014
- Vasilis Vryniotis
- . 6 Feedback
By now most of you have got heard/performed the 2048 recreation by Gabriele Cirulli. It’s a easy however extremely addictive board recreation which requires you to mix the numbers of the cells in an effort to attain the quantity 2048. As anticipated the issue of the sport will increase as extra cells are full of excessive values. Personally although I spent a good period of time taking part in the sport, I used to be by no means capable of attain 2048. So the pure factor to do is to attempt to develop an AI solver in JAVA to beat the 2048 recreation. 🙂
On this article I’ll briefly talk about my method for constructing the Synthetic Intelligence Solver of Recreation 2048, I’ll describe the heuristics that I used and I’ll present the entire code which is written in JAVA. The code is open-sourced below GPL v3 license and you’ll obtain it from Github.
Growing the 2048 Recreation in JAVA
The unique recreation is written in JavaScript, so I needed to rewrite it in JAVA from scratch. The primary concept of the sport is that you’ve got a 4×4 grid with Integer values, all of that are powers of two. Zero valued cells are thought-about empty. At each level throughout the recreation you’ll be able to transfer the values in direction of 4 instructions Up, Down, Proper or Left. Once you carry out a transfer all of the values of the grid transfer in direction of that course and so they cease both after they attain the borders of the grid or after they attain one other cell with non-zero worth. If that earlier cell has the identical worth, the 2 cells are merged into one cell with double worth. On the finish of each transfer a random worth is added within the board in one of many empty cells and its worth is both 2 with 0.9 likelihood or 4 with 0.1 likelihood. The sport ends when the participant manages to create a cell with worth 2048 (win) or when there are not any different strikes to make (lose).
Within the unique implementation of the sport, the move-merge algorithm is a bit sophisticated as a result of it takes under consideration all of the instructions. A pleasant simplification of the algorithm could be carried out if we repair the course in direction of which we will mix the items and rotate the board accordingly to carry out the transfer. Maurits van der Schee has just lately written an article about it which I imagine is price testing.
All of the courses are documented with Javadoc feedback. Under we offer a excessive degree description of the structure of the implementation:
1. Board Class
The board class comprises the primary code of the sport, which is liable for transferring the items, calculating the rating, validating if the sport is terminated and many others.
2. ActionStatus and Path Enum
The ActionStatus and the Path are 2 important enums which retailer the result of a transfer and its course accordingly.
3. ConsoleGame Class
The ConsoleGame is the primary class which permits us to play the sport and check the accuracy of the AI Solver.
4. AIsolver Class
The AIsolver is the first class of the Synthetic Intelligence module which is liable for evaluating the subsequent greatest transfer given a selected Board.
Synthetic Intelligence Methods: Minimax vs Alpha-beta pruning
A number of approaches have been printed to unravel mechanically this recreation. Probably the most notable is the one developed by Matt Overlan. To unravel the issue I attempted two totally different approaches, utilizing Minimax algorithm and utilizing Alpha-beta pruning.
Minimax Algorithm
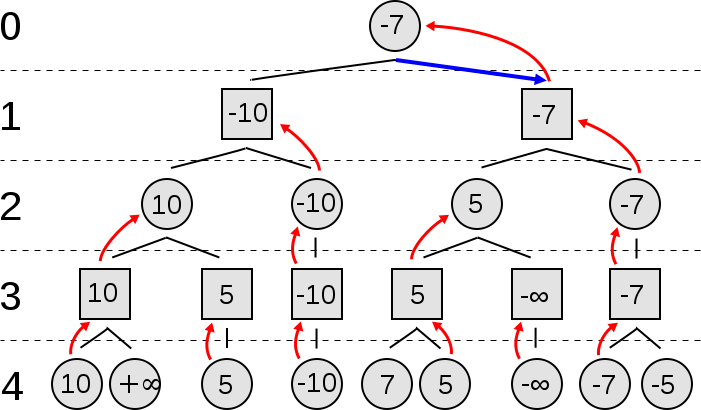
The Minimax is a recursive algorithm which can be utilized for fixing two-player zero-sum video games. In every state of the sport we affiliate a price. The Minimax algorithm searches by way of the house of potential recreation states making a tree which is expanded till it reaches a selected predefined depth. As soon as these leaf states are reached, their values are used to estimate those of the intermediate nodes.
The fascinating concept of this algorithm is that every degree represents the flip of one of many two gamers. With a view to win every participant should choose the transfer that minimizes the opponent’s most payoff. Here’s a good video presentation of the minimax algorithm:
Under you’ll be able to see pseudocode of the Minimax Algorithm:
operate minimax(node, depth, maximizingPlayer) if depth = 0 or node is a terminal node return the heuristic worth of node if maximizingPlayer bestValue := -∞ for every baby of node val := minimax(baby, depth - 1, FALSE)) bestValue := max(bestValue, val); return bestValue else bestValue := +∞ for every baby of node val := minimax(baby, depth - 1, TRUE)) bestValue := min(bestValue, val); return bestValue (* Preliminary name for maximizing participant *) minimax(origin, depth, TRUE)
Alpha-beta pruning
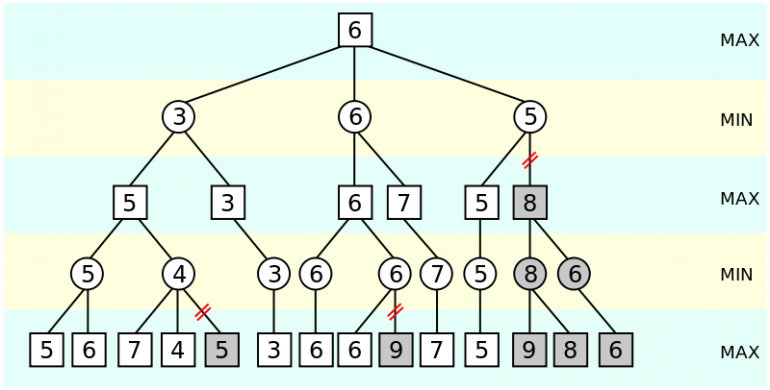
The Alpha-beta pruning algorithm is an enlargement of minimax, which closely decreases (prunes) the variety of nodes that we should consider/develop. To realize this, the algorithm estimates two values the alpha and the beta. If in a given node the beta is lower than alpha then the remainder of the subtrees could be pruned. Here’s a good video presentation of the alphabeta algorithm:
Under you’ll be able to see the pseudocode of the Alpha-beta pruning Algorithm:
operate alphabeta(node, depth, α, β, maximizingPlayer) if depth = 0 or node is a terminal node return the heuristic worth of node if maximizingPlayer for every baby of node α := max(α, alphabeta(baby, depth - 1, α, β, FALSE)) if β ≤ α break (* β cut-off *) return α else for every baby of node β := min(β, alphabeta(baby, depth - 1, α, β, TRUE)) if β ≤ α break (* α cut-off *) return β (* Preliminary name *) alphabeta(origin, depth, -∞, +∞, TRUE)
How AI is used to unravel the Recreation 2048?
With a view to use the above algorithms we should first determine the 2 gamers. The primary participant is the one who performs the sport. The second participant is the pc which randomly inserts values within the cells of the board. Clearly the primary participant tries to maximise his/her rating and obtain the 2048 merge. Alternatively the pc within the unique recreation just isn’t particularly programmed to dam the consumer by deciding on the worst potential transfer for him however quite randomly inserts values on the empty cells.
So why we use AI strategies which remedy zero-sum video games and which particularly assume that each gamers choose the absolute best transfer for them? The reply is easy; even though it’s only the primary participant who tries to maximise his/her rating, the alternatives of the pc can block the progress and cease the consumer from finishing the sport. By modeling the conduct of the pc as an orthological non-random participant we be certain that our selection can be a stable one independently from what the pc performs.
The second essential half is to assign values to the states of the sport. This drawback is comparatively easy as a result of the sport itself offers us a rating. Sadly attempting to maximise the rating by itself just isn’t a superb method. One motive for that is that the place of the values and the variety of empty valued cells are essential to win the sport. For instance if we scatter the massive values in distant cells, it could be actually tough for us to mix them. Moreover if we’ve got no empty cells obtainable, we threat shedding the sport at any minute.
For all of the above causes, a number of heuristics have been urged such because the Monoticity, the smoothness and the Free Tiles of the board. The primary concept is to not use the rating alone to guage every game-state however as an alternative assemble a heuristic composite rating that features the aforementioned scores.
Lastly we should always be aware that although I’ve developed an implementation of Minimax algorithm, the massive variety of potential states makes the algorithm very gradual and thus pruning is critical. In consequence within the JAVA implementation I exploit the enlargement of Alpha-beta pruning algorithm. Moreover not like different implementations, I don’t prune aggressively the alternatives of the pc utilizing arbitrary guidelines however as an alternative I take all of them under consideration in an effort to discover the absolute best transfer of the participant.
Growing a heuristic rating operate
With a view to beat the sport, I attempted a number of totally different heuristic features. The one which I discovered most helpful is the next:
personal static int heuristicScore(int actualScore, int numberOfEmptyCells, int clusteringScore) {
int rating = (int) (actualScore+Math.log(actualScore)*numberOfEmptyCells -clusteringScore);
return Math.max(rating, Math.min(actualScore, 1));
}
The above operate combines the precise rating of the board, the variety of empty cells/tiles and a metric referred to as clustering rating which we’ll talk about later. Let’s see every part in additional element:
- Precise Rating: For apparent causes, after we calculate the worth of a board we’ve got to take into consideration its rating. Boards with increased scores are typically most popular compared to boards with decrease scores.
- Variety of Empty Cells: As we talked about earlier, conserving few empty cells is essential to make sure that we is not going to lose the sport within the subsequent strikes. Board states with extra empty cells are typically most popular compared to others with fewer. A query rises regarding how would we worth these empty cells? In my resolution I weight them by the logarithm of the particular rating. This has the next impact: The decrease the rating, the much less essential it’s to have many empty cells (It is because initially of the sport combining the cells is pretty straightforward). The upper the rating, the extra essential it’s to make sure that we’ve got empty cells in our recreation (It is because on the finish of the sport it’s extra possible to lose because of the lack of empty cells.
- Clustering Rating: We use the clustering rating which measures how scattered the values of our board are. When cells with related values are shut they’re simpler to mix that means it’s tougher to lose the sport. On this case the clustering rating has a low worth. If the values of the board are scattered, then this rating will get a really massive worth. This rating is subtracted from the earlier two scores and acts like a penalty that ensures that clustered boards can be most popular.
Within the final line of the operate we be certain that the rating is non-negative. The rating must be strictly constructive if the rating of the board is constructive and 0 solely when the board of the rating is zero. The max and min features are constructed in order that we get this impact.
Lastly we should always be aware that when the participant reaches a terminal recreation state and no extra strikes are allowed, we don’t use the above rating to estimate the worth of the state. If the sport is received we assign the best potential integer worth, whereas if the sport is misplaced we assign the bottom non damaging worth (0 or 1 with related logic as within the earlier paragraph).
Extra in regards to the Clustering Rating
As we mentioned earlier the clustering rating measures how a lot scattered are the values of the board and acts like a penalty. I constructed this rating in such a method in order that it incorporates ideas/guidelines from customers who “mastered” the sport. The primary urged rule is that you just attempt to preserve the cells with related values shut in an effort to mix them simpler. The second rule is that prime valued cells must be shut to one another and never seem in the course of the board however quite on the edges or corners.
Let’s see how the clustering rating is estimated. For each cell of the board we estimate the sum of absolute variations from its neighbors (excluding the empty cells) and we take the common distinction. The explanation why we take the averages is to keep away from counting greater than as soon as the impact of two neighbor cells. The overall clustering rating is the sum of all these averages.
The Clustering Rating has the next attributes:
- It will get excessive worth when the values of the board are scattered and low worth when cells with related values are shut to one another.
- It doesn’t overweigh the impact of two neighbor cells.
- Cells within the margins or corners have fewer neighbors and thus decrease scores. In consequence when the excessive values are positioned close to the margins or corners they’ve smaller scores and thus the penalty is smaller.
The accuracy of the algorithm
As anticipated the accuracy (aka the share of video games which might be received) of the algorithm closely is dependent upon the search depth that we use. The upper the depth of the search, the upper the accuracy and the extra time it requires to run. In my exams, a search with depth 3 lasts lower than 0.05 seconds however offers 20% likelihood of profitable, a depth of 5 lasts a few 1 second however offers 40% likelihood of profitable and at last a depth of seven lasts 27-28 seconds and offers about 70-80% likelihood of profitable.
Future expansions
For these of you who’re all in favour of enhancing the code listed below are few issues that you could look into:
- Enhance the Pace: Bettering the velocity of the algorithm will can help you use bigger depth and thus get higher accuracy.
- Create Graphics: There’s a good motive why Gabriele Cirulli’s implementation grew to become so well-known. It’s good trying! I didn’t trouble creating a GUI however I quite print the outcomes on console which makes the sport tougher to comply with and to play. Creating a pleasant GUI is a should.
- Tune Heuristics: As I discussed earlier, a number of customers have urged totally different heuristics. One can experiment with the way in which that the scores are calculated, the weights and the board traits which might be taken under consideration. My method of measuring the cluster rating is meant to mix different options similar to Monotonicity and Smoothness, however there may be nonetheless room for enchancment.
- Tuning the Depth: One may attempt to tune/modify the depth of the search relying on the sport state. Additionally you need to use the Iterative deepening depth-first search algorithm which is thought to enhance the alpha-beta pruning algorithm.
Don’t neglect to obtain the JAVA code from Github and experiment. I hope you loved this put up! Should you did please take a second to share the article on Fb and Twitter. 🙂

