November 12, 2020
I just lately encountered this cool paper in a studying group presentation:
It is frankly taken me a very long time to know what was happening, and it took me weeks to jot down this half-decent clarification of it. The first notes I wrote adopted the logic of the paper extra, this on this publish I believed I’d simply give attention to the excessive degree concept, after which hopefully the paper is extra easy. I wished to seize the important thing concept, with out the distractions of RNN hidden states, and many others, which I discovered complicated to consider.
POMDP setup
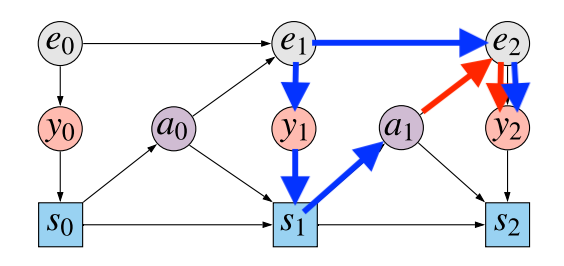
To start out with the fundamentals, this paper offers with the partially noticed Markov choice course of (POMDP) setup. The diagram beneath illustrates what is going on on:
The gray nodes $e_t$ present the unobserved state of the atmosphere at every timestep $t=0,1,2ldots$. At every timestep the agent observes $y_0$ which is dependent upon the present state of the atmosphere (red-ish nodes). The agent then updates their state $s_t$ primarily based on its previous state $s_{t-1}$, the brand new statement $y_t$, and the earlier motion taken $a_{t-1}$. That is proven by the blue squares (they’re squares, signifying that this node relies upon deterministically on its dad and mom). Then, primarily based on the agent’s state, it chooses an motion $a_t$ from by sampling from coverage $pi(a_tvert s_t)$. The motion influences how the atmosphere’s state, $e_{t+1}$ modifications.
We assume that the agent’s final purpose is to maximise reward on the final state at time $T$, which we assume is a deterministic perform of the statement $r(y_T)$. Consider this reward because the rating in an atari sport, which is written on the display whose contents are made accessible in $y_t$.
The final word purpose
Let’s begin by stating what we in the end would really like estimate from the information now we have. The idea is that we sampled the information utilizing some coverage $pi$, however we wish to have the ability to say how properly a unique coverage $tilde{pi}$ would do, in different phrases, what could be the anticipated rating at time $T$ if as an alternative of $pi$ we used a unique coverage $tilde{pi}$.
What we’re fascinated about, is a causal/counterfactual question:
$$
mathbb{E}_{tausimtilde{p}}[r(y_T)],
$$
the place $tau = [(s_t, y_t, e_t, a_t) : t=0ldots T]$ denotes a trajectory or rollout as much as time $T$, and $tilde{p}$ denotes the generative course of when utilizing coverage $tilde{pi}$, that’s:
$$
tilde{p}(tau) = p(e_0)p(y_0vert e_0) tilde{pi}(a_0vert s_0) p(s_0)prod_{t=1}^T p(e_tvert a_{t-1}, e_{t-1}) p(y_tvert e_t) tilde{pi}(a_tvert s_t) delta (s_t – g(s_{t-1}, y_t))
$$
I known as this a causal or counterfactual question, as a result of we’re fascinated about making predictions beneath a unique distribution $tilde{p}$ than $p$ which now we have observations from. The distinction between $tilde{p}$ and $p$ may be known as an intervention, the place we change particular elements within the information producing course of with completely different ones.
There are – no less than – two methods one might go about estimating such counterfactual distribution:
- model-free, through significance sampling. This technique tries to immediately estimate the causal question by calculating a weighted common over the noticed information. The weights are given by the ratio between $tilde{pi}(a_tvert s_t)$, the likelihood by which $tilde{pi}$ would select an motion and $pi(a_tvert s_t)$, the likelihood it was chosen by the coverage that we used to gather the information. An awesome paper explaining how this works is (Bottou et al, 2013). Significance sampling because the benefit that we do not have to construct any mannequin of the atmosphere, we will immediately consider the typical reward from the samples now we have, utilizing solely $pi$ and $tilde{pi}$ to calculate the weights. The draw back, nevertheless, is that significance sampling usually extremely excessive variance estimate, and is just dependable if $tilde{pi}$ and $pi$ are very shut.
- model-based, through causal calculus. If attainable, we will use do-calculus to specific the causal question in an alternate manner, utilizing varied conditional distributions estimated from the noticed information. This strategy has the drawback that it requires us construct a mannequin from the information first. We then use the conditional distributions discovered from the information to approximate the amount of curiosity by plugging them into the formulation we acquired from do-calculus. If our fashions are imperfect, these imperfections/approximation errors can compound when the causal estimand is calculated, doubtlessly resulting in massive biases and inaccuracies. However, our fashions could also be correct sufficient to extrapolate to conditions the place significance weighting could be unreliable.
On this paper, we give attention to fixing the issue with causal calculus. This requires us to construct a mannequin of noticed information, which we will then use to make causal predictions. The important thing query this paper asks is
How a lot of the information do now we have to mannequin to have the ability to make the sorts of causal inferences we want to make?
Choice 1: mannequin (virtually) every thing
A technique we will reply the question above is to mannequin the joint distribution of every thing, or largely every thing, that we will observe. For instance, we might construct a full autoregressive mannequin of observations $y_t$ conditioned on actions $a_t$. In essence this could quantity to becoming a mannequin to $p(y_{0:T}vert a_{0:T})$.
If we had such mannequin, we’d theoretically be capable of make causal predictions, for causes I’ll clarify later. Nevertheless, this selection is dominated out within the paper as a result of we assume the observations $y_t$ are very excessive dimensional, akin to photographs rendered in a pc sport. Thus, modelling the joint distribution of the entire statement sequence $y_{1:T}$ precisely is hopeless and would require a number of information. Subsequently, we want to get away with out modelling the entire statement sequence $y_{1:T}$, which brings us to partial fashions.
Choice 2: partial fashions
Partial fashions attempt to keep away from modelling the joint distribution of high-dimensional observations $y_{1:T}$ or agent-state sequences $s_{0:T}$, and give attention to modelling immediately the distribution of $r(y_T)$ – i.e. solely the reward part of the final statement, given the action-sequence $a_{0:T}$. That is clearly loads simpler to do, as a result of $r(y_T)$ is assumed to be a low-dimensional facet of the total statement $y_T$, so all now we have to be taught is a mannequin of a scalar conditioned on a sequence of actions $q_theta(r(y_T)vert a_{0:T})$. We all know very properly how you can match such fashions to practical quantities of information.
Nevertheless, if we do not embrace both $y_t$ or $s_t$ in our mannequin, we cannot be capable of make the counterfactual inferences we wished to make within the first place. Why? Let’s take a look at he information producing course of as soon as extra:
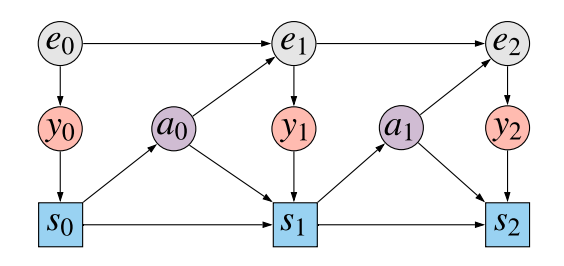
We try to mannequin the causal affect of actions $a_0$ and $a_1$ on the end result $y_2$. Let’s give attention to $a_1$. $y_2$ is clearly statistically depending on $a_1$. Nevertheless, this statistical dependence emerges resulting from utterly completely different results:
- causal affiliation: $a_1$ influences the state of the atmosphere $e_2$, leading to an statement $y_2$. Subsequently, $a_1$ has an direct causal impact on $y_2$, mediated by $e_2$
- spurious affiliation resulting from confounding: The unobserved hidden state $e_1$ is a confounder between the motion $a_1$ and the statement $y_2$. The state $e_1$ has an oblique causal impact on $a_1$ mediated by the statement $y_1$ and the agent’s state $s_1$. Equally $e_1$ has an oblique impact on $y_2$ mediated by $e_2$.
I illustrated these two sources of statistical affiliation by colour-coding the completely different paths within the causal graph. The blue path is the confounding path: correlation is induced as a result of each $a_1$ and $y_2$ have $e_1$ as causal ancestor. The pink path is the causal path: $a_1$ not directly influences $y_2$ through the hidden state $e_2$.
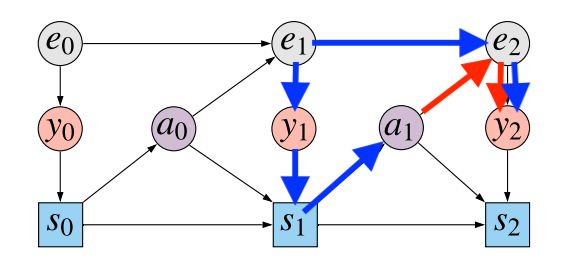
If we want to appropriately consider the consequence of fixing insurance policies, now we have to have the ability to disambiguate between these two sources of statistical affiliation, do away with the blue path, and solely take the pink path under consideration. Sadly, this isn’t attainable in a partial mannequin, the place we solely mannequin the distribution of $y_2$ conditional on $a_0$ and $a_1$.
If we wish to draw causal inferences, we should mannequin the distribution of no less than one variable alongside blue path. Clearly, $y_1$ and $s_1$ are theoretically observable, and are on the confounding path. Including both of those to our mannequin would enable us to make use of the backdoor adjustment formulation (defined within the paper). Nevertheless, this could take us again to Choice 1, the place now we have to mannequin the joint distribution of both sequences of observations $y_{0:T}$ or sequences of states $s_{0:T}$, each assumed to be high-dimensional and tough to mannequin.
Choice 3: causally appropriate partial fashions
So we lastly acquired to the core of what’s proposed within the paper: a type of halfway-house between modeling every thing and modeling too little. We’re going to mannequin sufficient variables to have the ability to consider causal queries, whereas holding the dimensionality of the mannequin now we have to suit low. To do that, we alter the information producing course of barely – by splitting the coverage into two phases:
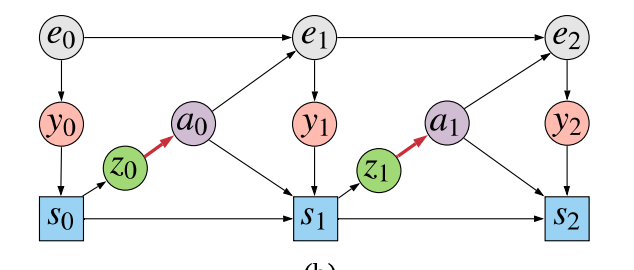
The agent first generates $z_t$ from the state $s_t$, after which makes use of the sampled $z_t$ worth to decide $a_t$. One can perceive $z_t$ as being a stochastic bottleneck between the agent’s high-dimensional state $s_t$, and the low-dimensional motion $a_t$. The idea is that the sequence $z_{0:T}$ needs to be loads simpler to mannequin than both $y_{0:T}$ or $s_{0:T}$. Nevertheless, if we now construct a mannequin $p(r(y_T), z_{0:T} vert a_{0:T})$ are actually in a position to make use of this mannequin consider the causal queries of curiosity, thanks for the backdoor adjustment formulation. For how you can exactly do that, please consult with the paper.
Intuitively, this strategy helps by including a low-dimensional stochastic node alongside the confounding path. This permits us to compensate for confounding, with out having to construct a full generative mannequin of sequences of high-dimensional variables. It permits us to unravel the issue we have to clear up with out having to unravel a ridiculously tough subproblem.