This publish is written with my PhD scholar and now visitor writer Patrik Reizinger and is a component 4 of a collection of posts on causal inference:
A technique to consider causal inference is that causal fashions require a extra fine-grained fashions of the world in comparison with statistical fashions. Many causal fashions are equal to the identical statistical mannequin, but assist totally different causal inferences. This publish elaborates on this level, and makes the connection between causal and statistical fashions extra exact.
Do you bear in mind these combinatorics issues from college the place the query was what number of methods exist to get from a begin place to a goal subject on a chessboard? And you may solely transfer one step proper or one step down. When you bear in mind, then I have to admit that we’ll not contemplate issues like that. However its (one doable) takeaway really may also help us to know Markov factorizations.
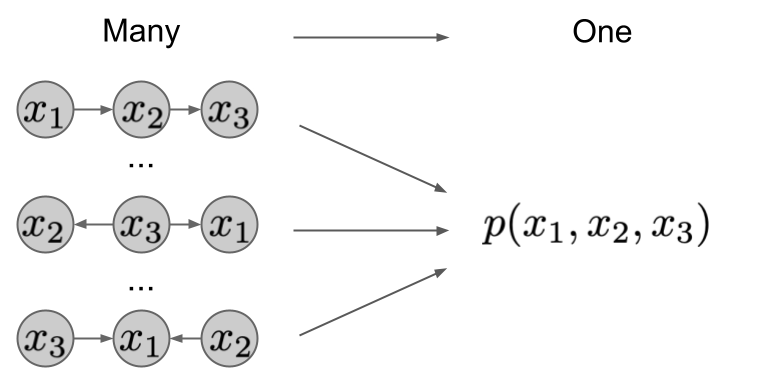
You recognize, it’s completely detached the way you traversed the chessboard, the consequence is similar. So we are able to say that – from the attitude of goal place and the method of getting there – it is a many-to-one mapping. The identical holds for random variables and causal generative fashions.
When you’ve got a bunch of random variables – let’s name them $X_1, X_2, dots, X_n$ -, their joint distribution is $p left(X_1, X_2, dots, X_n proper) $. When you invoke the chain rule of likelihood, you’ll have a number of choices to precise this joint as a product of things:
$$
p left(X_1, X_2, dots, X_n proper) = prod p(X_{pi_i}vert X_{pi_1}, ldots, X_{pi_{i-1}}),
$$
the place $pi_i$ is a permutation of indices. Since you are able to do this for any permutation $pi$, the mapping between such factorizations and the joint distribution they specific is many-to-one. As you possibly can see this within the picture under. The totally different factorizations induce a unique graph, however have the identical joint distribution.
Since you’re studying this publish, chances are you’ll already remember that in causal inference we regularly discuss a causal factorization, which seems to be like
$$
p left(X_1, X_2, dots, X_n proper) = prod_{i=1}^{n} pleft(X_i | X_{mathrm{pa}(i)}proper),
$$
the place $mathrm{pa}(X_i)$ denotes the causal dad and mom of node $X_i$. That is certainly one of many doable methods you possibly can factorize the joint distribution, however we contemplate this one particular. Within the current work, Schölkopf et al. name it a disentangled mannequin. What are disentangled fashions? Disentangled components describe unbiased elements of the mechanism that generated the info. And they don’t seem to be unbiased since you factored them on this means, however you had been searching for this factorization as a result of its components are unbiased.
In different phrases, for each joint distribution there are numerous doable factorizations, however we assume that just one, the causal or disentangled factorization, describes the true underlying course of that generated the info.
Let’s contemplate an instance for disentangled fashions. We need to mannequin the joint distribution of altitude $A$ and temperature $T$. On this case, the causal path is $A rightarrow T$ – if the altitude adjustments, the distribution of the temperature will change too. However you can not change the altitude by artificially heating a metropolis – in any other case all of us would take pleasure in views as in Miami; international warming is actual however fortuitously has no altitude-changing impact.
Ultimately, we get the factorization of $p(A)p(T|A)$. The vital insights listed below are the solutions to the query: What will we count on from these components? The previously-mentioned Schölkopf et al. paper calls the principle takeaway the Unbiased Causal Mechanisms (ICM) Precept, i.e.
By conditioning on the dad and mom of any issue within the disentangled mannequin, the issue will neither have the ability to provide you with additional details about different components nor is ready to affect them.
Within the above instance, because of this in the event you contemplate totally different international locations with their altitude distributions, you possibly can nonetheless use the identical $p(T|A),$ i.e., the components generalize properly. For no affect, the instance holds straight above the ICM Precept. Moreover, understanding any of the components – e.g. $p(A)$ – will not inform something in regards to the different (no data). If you understand which nation you’re in, so may have no clue in regards to the local weather (in the event you consulted the web site of the corresponding climate company, that is what I name dishonest). Within the different path, regardless of being the top-of-class scholar in local weather issues, you will not have the ability to inform the nation if any person says to you that right here the altitude is 350 meters and the temperature is 7°C!
Statistical vs causal inference
We mentioned Markov factorizations, as they assist us perceive the philosophical distinction between statistical and causal inference. The wonder, and a supply of confusion, is that one can use Markov factorizations in each paradigms.
Nonetheless, whereas utilizing Markov factorizations is non-obligatory for statistical inference, it’s a should for causal inference.
So why would a statistical inference individual use Markov factorizations? As a result of they make life simpler within the sense that you do not want to fret about too excessive electricty prices. Particularly, factorized fashions of knowledge might be computationally far more environment friendly. As an alternative of modeling a joint distribution straight, which has loads of parameters – within the case of $n$ binary variables, that’s $2^n-1$ totally different values -, a factorized model might be fairly light-weight and parameter-efficient. If you’ll be able to factorize the joint in a means that you’ve 8 components with $n/8$ variables every, then you possibly can describe your mannequin with $8times2^{n/8}-1$ parameters. If $n=16$, that’s $65,535$ vs $31$. Equally, representing your distibution in a factorized type offers rise to environment friendly, general-purpose message-passing algorithms, resembling perception propagation or expectation propagation.
Alternatively, causal inference individuals actually need this, in any other case, they’re misplaced. As a result of with out Markov factorizations, they can’t actually formulate causal claims.
A causal practicioner makes use of Markov factorizations, as a result of this fashion she is ready to purpose about interventions.
When you do not need the disentangled factorization, you can not mannequin the impact of interventions on the true mechanisms that make the system tick.
Connection to area adaptation
In plain machine studying lingo, what you need to do is area adaptation, that’s, you need to draw conclusions a couple of distribution you didn’t observe (these are the interventional ones). The Markov factorization prescribes methods through which you count on the distribution to alter – one issue at a time – and thus the set of distributions you need to have the ability to robustly generalise to or draw inferences about.
Do calculus
Do-caclculus, the subject of the first publish within the collection, might be comparatively merely described utilizing Markov factorizations. As you bear in mind, $mathrm{do}(X=x)$ implies that we set the variable $X$ to the worth $x$, which means that the distribution of that variable $p(X)$ collapses to a degree mass. We will mannequin this intervention mathematically by changing the issue $p( x vert mathrm{pa}(X))$ by a Dirac-delta $delta_x$, ensuing within the deletion of all incoming edges of the intervened components within the graphical mannequin. We then marginalise over $x$ to calculate the joint distribution of the remaining variables. For instance, if we now have two variables $x$ and $y$ we are able to write:
$$
p(yvert do(X=x_0)) = int p(x,y) frac{delta(x – x_0)}{p(xvert y)} dx
$$
SEMs, Markov factorization, and the reparamtrization trick
When you’ve learn the earlier components on this collection, you may know that Markov factorizations aren’t the one instrument we use in causal inference. For counterfactuals, we used structural equation fashions (SEMs). On this half we are going to illustrate the connection between these with a tacky reference to the reparametrization trick utilized in VAEs amongst others.
However earlier than that, let’s recap SEMs. On this case, you outline the connection between the kid node and its dad and mom through a practical task. For node $X$ with dad and mom $mathrm{pa}(X)$ it has the type of
$$
X = f(mathrm{pa}(X), epsilon),
$$
with some noise $epsilon.$ Right here, it’s best to learn “=” within the sense of an assigment (like in Python), in arithmetic, this must be “:=”.
The above equation expresses the conditional likelihood $ pleft(X| mathrm{pa}(X)proper)$ as a deterministic operate of $X$ and a few noise variable $epsilon$. Wait a second…, is not it the identical factor what the reparametrization trick does? Sure it’s.
So the SEM formulation (referred to as the implicit distribution) is expounded through the reparametrization trick to the conditional likelihood of $X$ given its dad and mom.
Lessons of causal fashions
Thus, we are able to say {that a} SEM is a conditional distribution, and vica versa. Okay, however how do the units of those constructs relate to one another?
When you’ve got a SEM, then you possibly can learn off the conditional, which is distinctive. Alternatively, yow will discover extra SEMs for a similar conditional. Simply as you possibly can specific a conditional distribution in a number of other ways utilizing totally different reparametrizations, it’s doable to precise the identical Markov factorization by a number of SEMs. Contemplate for instance that in case your distribution is $mathcal{N}(mu,sigma),$ then multiplying it by -1 offers you a similar distribution. On this sense, SEMs are a richer class of fashions than Markov factorizations, thus they permit us to make inferences (counterfactual) which we weren’t capable of specific within the extra coarse grained language of Markov Factorizations.
As we mentioned above, a single joint distribution has a number of legitimate Markov factorizations, and the identical Markov factorization might be expressed as totally different SEMs. We will consider joint distributions, Markov factorizations, and SEMs as more and more fine-grained mannequin lessons: joint distributions $subset$ Markov facorizations $subset$ SEMs. The extra elements of the info producing course of you mannequin, the extra elaborate the set of inferences you can also make turn out to be. Thus, Joint distributions assist you to make predictions below no mechanism shift, Markov factorizations assist you to mannequin interventions, SEMs assist you to make counterfactual statements.
The value you pay for extra expressive fashions is that in addition they get typically a lot tougher to estimate from knowledge. The truth is, some elements of causal fashions are inconceivable to deduce from i.i.d. observational knowledge. Furthermore, some counterfactual inferences are experimentally not verifiable.